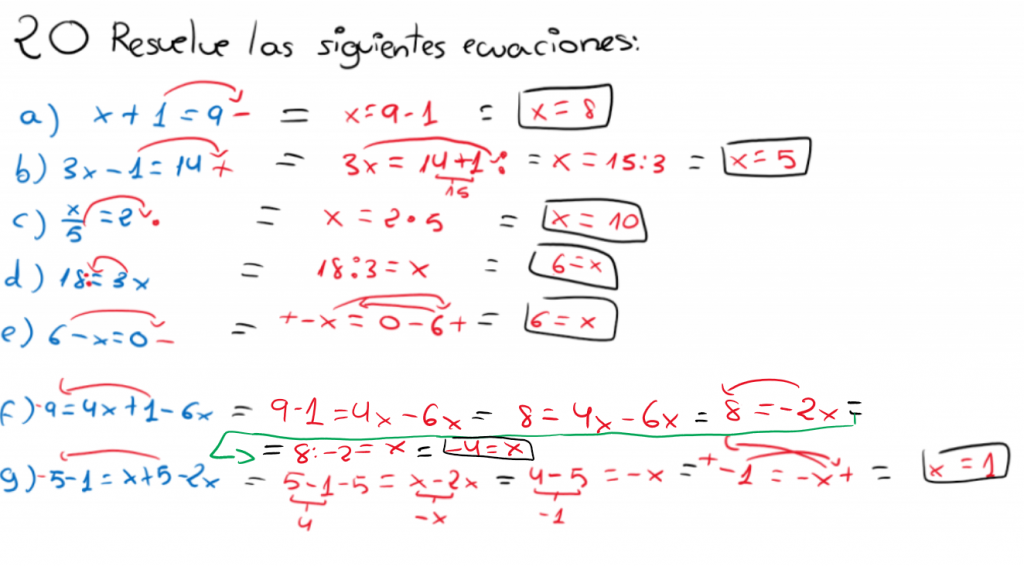Letras en vez de números
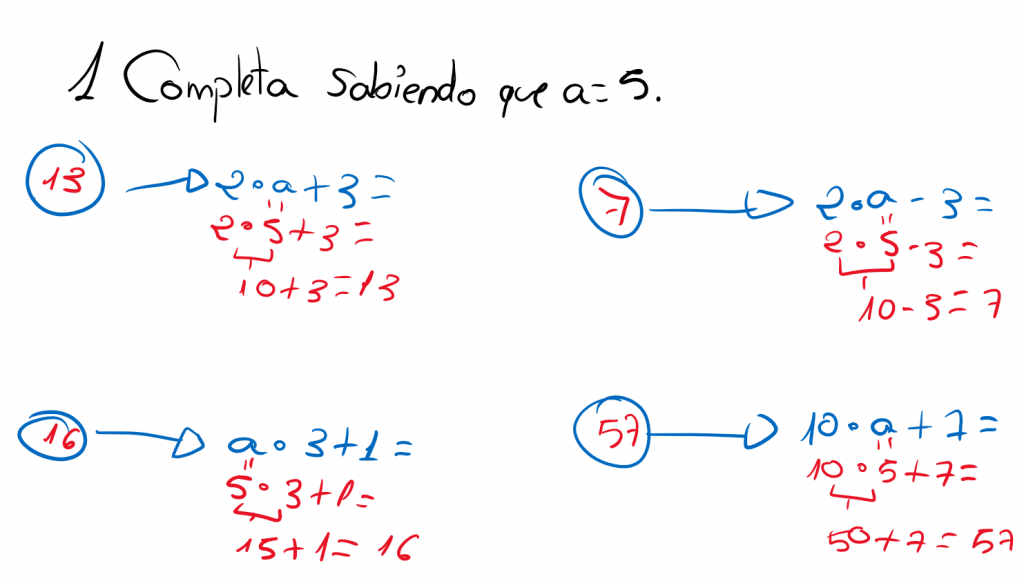
Cuando las letras expresan números, las trataremos como tales en cuanto a las operaciones y propiedades.
El álgebra es la parte de las matemáticas que se ocupa de estudiar el comportamiento de las expresiones con letras y números, por tanto se incluirán las letras en matemáticas que como dice el párrafo anterior, se las trata como números.
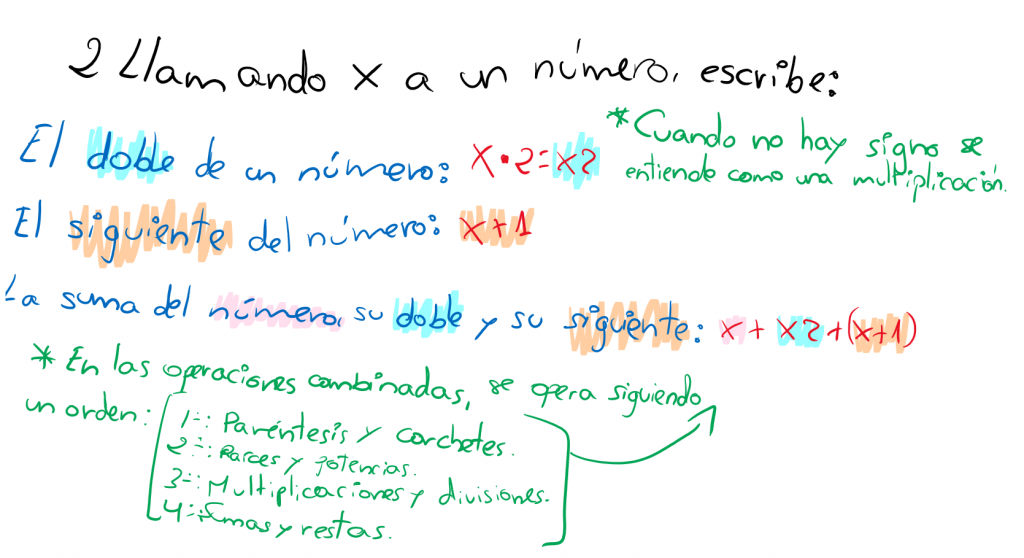
Expresiones algebraicas
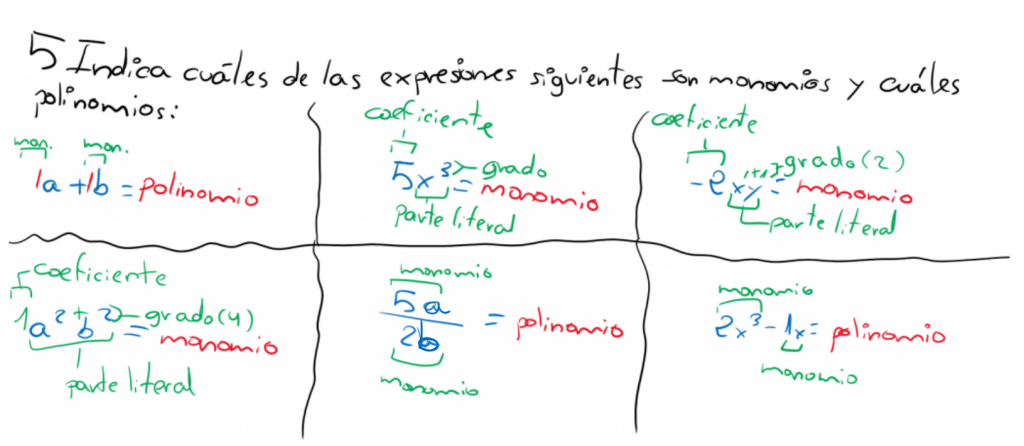
MONOMIOS:
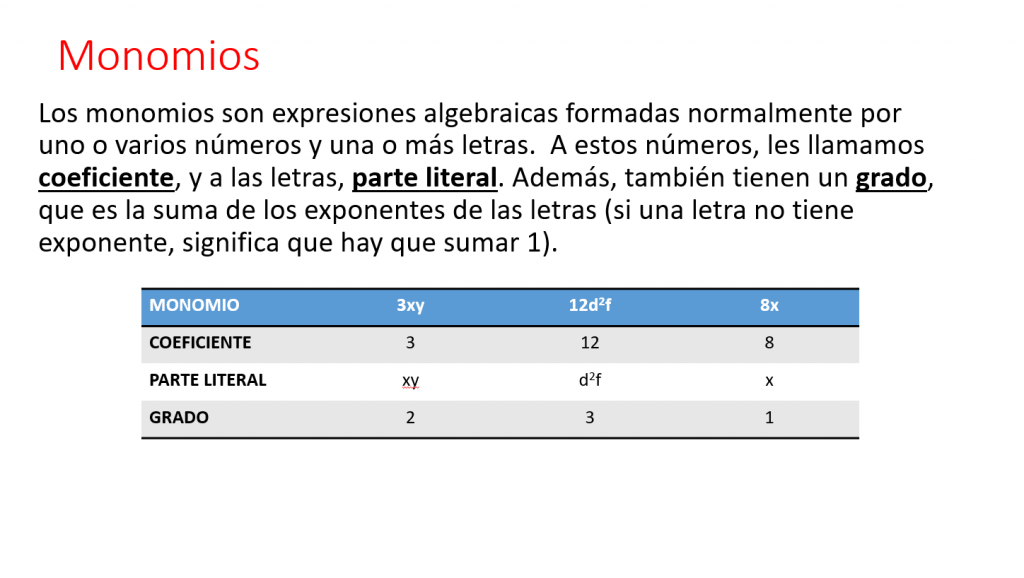
Un monomio consiste en el producto de un número conocido (coeficiente) por una o varias letras (partes literales). El grado de un monomio es la suma de los exponentes de la parte literal, 6 X4Y tiene como grado 5, porque la X está elevada a 4+1 que está elevada la Y (aunque no se indica).
En ocasiones, un monomio puede no tener coeficiente (número) visible lo cual significa que es 1 (X2y tiene como coeficiente un 1, pero no se indica). También puede no tener parte literal (5:7 tiene como coeficiente 5:7 y no tiene parte literal, por tanto, su grado es 0).

POLINOMIOS:
Un polinomio es la suma, resta, división y multiplicación indicada de varios números.
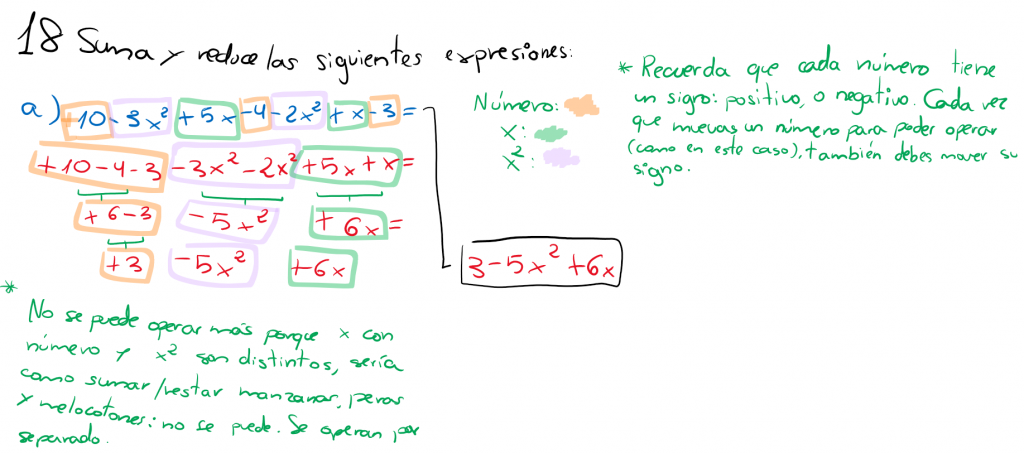
SUMA Y RESTA DE MONOMIOS Y POLINOMIOS:
Los monomios solo se pueden sumar o restar cuando son semejantes. Cuando no lo son, la operación se deja indicada (reducida todo lo posible hasta que no se pueda continuar operando).
Los monomios son semejantes si la parte literal de estos es idéntica en todos los casos.

Expresiones algebraicas II
MULTIPLICACIÓN DE MONOMIOS
Un monomio es un producto. Por tanto, al multiplicar dos monomios obtenemos otro producto con más factores; es decir, otro monomio.
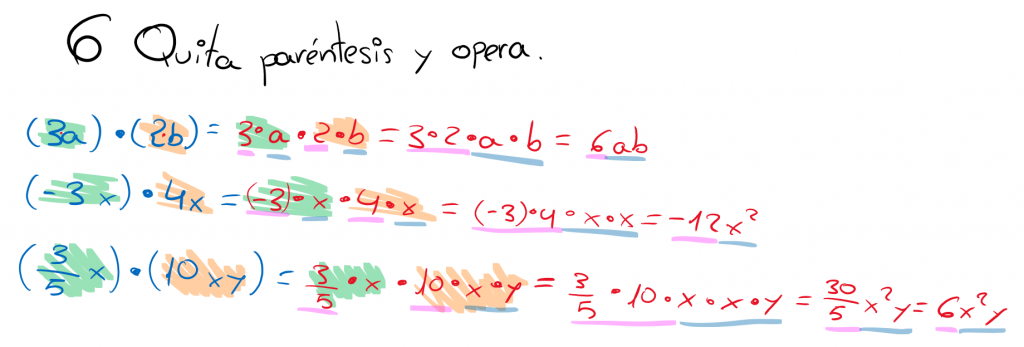
El producto de dos monomios es siempre otro monomio.

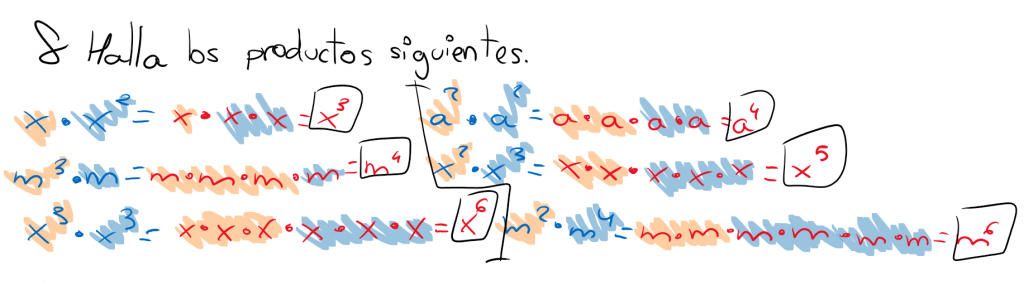
MULTIPLICACIÓN DE UN MONOMIO POR UN POLINOMIO
Como el polinomio es una suma o resta, aplicamos la propiedad distributiva; es decir, multiplicamos por cada sumando.
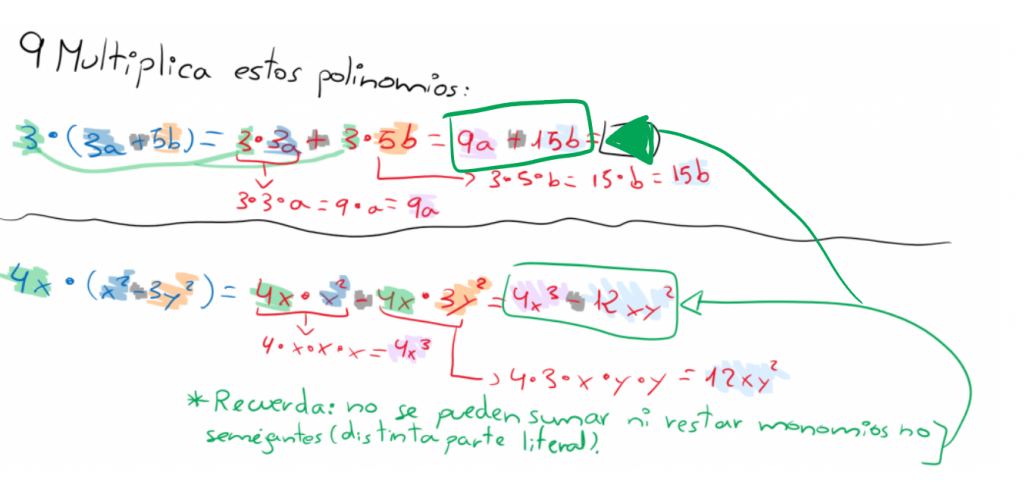
DIVISIÓN DE MONOMIOS
Al dividir dos monomios, se puede obtener:
- Un monomio.
- Otro número.
- Una fracción algebraica.
Hay dos formas de dividir monomios:
PRIMERA FORMA:
1º: se dividen los coeficientes de los monomios:
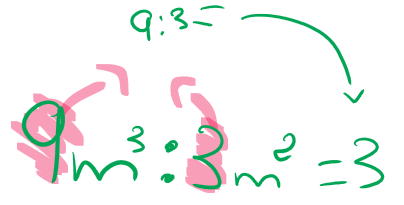
2º: se restan los exponentes de la parte literal (si no hay=1).
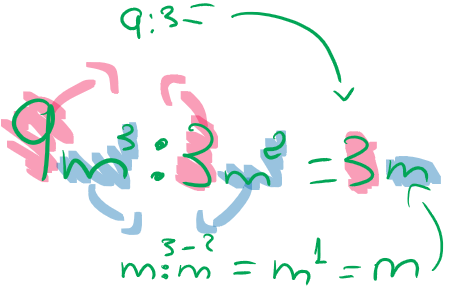
SEGUNDA FORMA:
Para dividir dos monomios, seguiremos aplicando lo que sabemos sobre operaciones con números.
Como comprobarás en los ejemplos que siguen, se pueden obtener diferentes tipos de resultados.
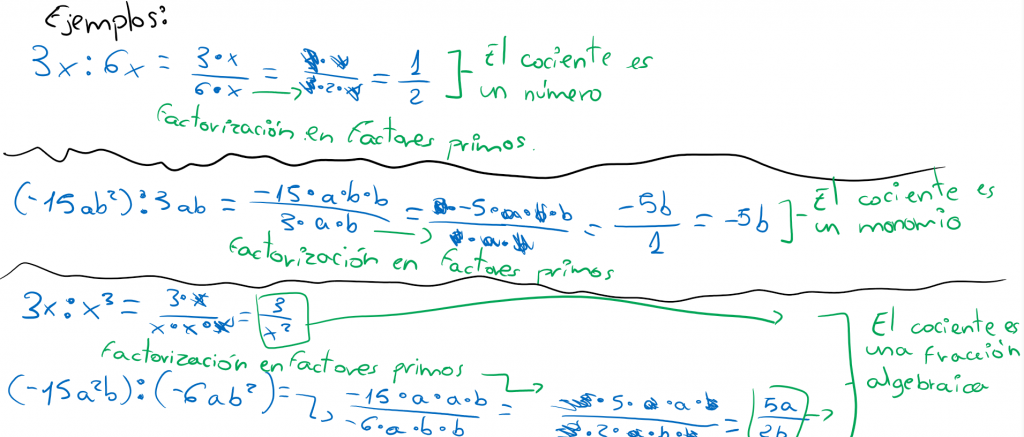
Repaso de lo visto hasta ahora.




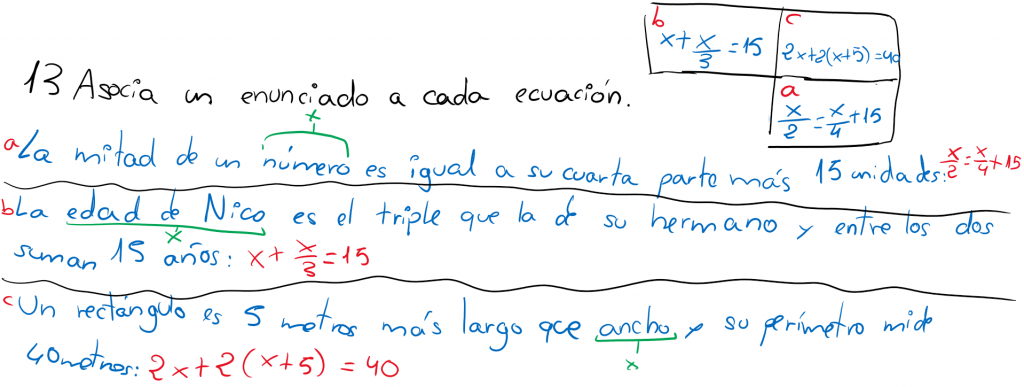
Ecuaciones
IGUALDADES ALGEBRAICAS: ecuaciones e identidades.
- Una ecuación es una igualdad entre expresiones algebraicas que se cumple solamente en ciertos valores de las letras.
- Una identidad es una igualdad algebraica que se cumple siempre, independientemente de los valores que tomen las letras.
ELEMENTOS DE UNA ECUACIÓN
- Miembros: son las expresiones que aparecen a cada lado del signo de igualdad.
- Términos: son los sumandos que forman los miembros.
- Incógnitas: son las letras que aparecen en los términos.
- Soluciones: son los valores que han de tomar las letras para que se cumpla la igualdad.
ECUACIONES EQUIVALENTES:
Dos ecuaciones son equivalentes cuando sus soluciones coinciden.
¿QUÉ ES RESOLVER UNA ECUCACIÓN?
Resolver una ecuación es encontrar sus soluciones. Es decir, averiguar los valores que deben tomar las incógnitas para que se cumpla la igualdad.


Primeras técnicas para la resolución de ecuaciones
RESOLUCIÓN DE LA ECUACIÓN x+a=b
Para resolver la ecuación x+a=b, restamos a (para anularla) en ambos miembros (para mantener la igualdad).
Regla:
Lo que está sumando en uno de los miembros, pasa restando al otro (esta es la regla que cumple lo leído justo arriba pero de una forma más práctica, por tanto el resultado es el mismo).
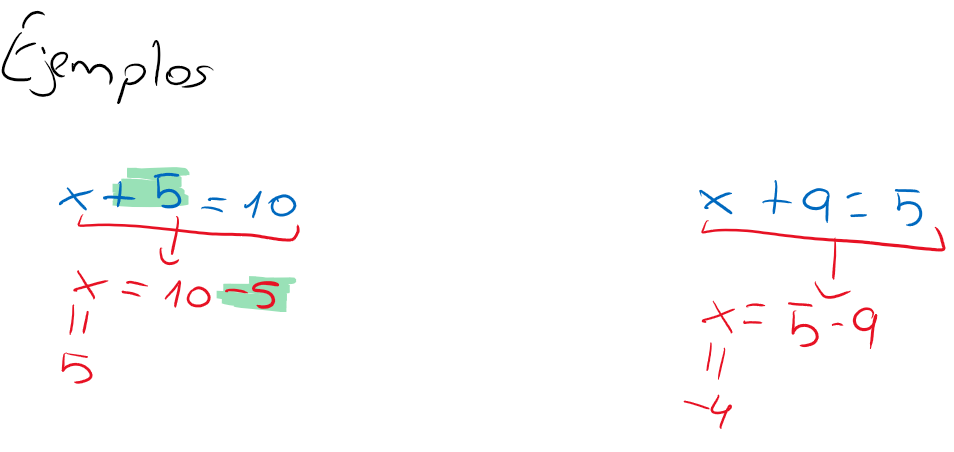
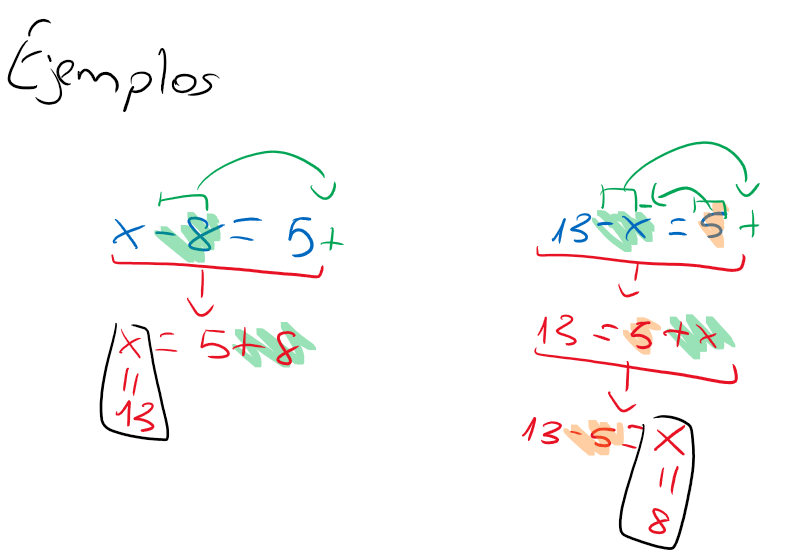
RESOLUCIÓN DE LA ECUACIÓN x-a=b
Para resolver la ecuación x-a=b, sumamos a (para anularla) en ambos miembros (para mantener la igualdad).
Regla:
Lo que está restando en uno de los miembros, pasa sumando al otro (esta es la regla que cumple lo leído justo arriba pero de una forma más práctica, por tanto el resultado es el mismo).
RESOLUCIÓN DE LA ECUACIÓN a·x=b
Para resolver la ecuación a·x=b, dividimos la a (para anularla) en ambos miembros (para mantener la igualdad) entre ambos.
Regla:
Lo que está multiplicando a un miembro (a todo él), pasa dividiendo al otro (esta es la regla que cumple lo leído justo arriba pero de una forma más práctica, por tanto el resultado es el mismo).
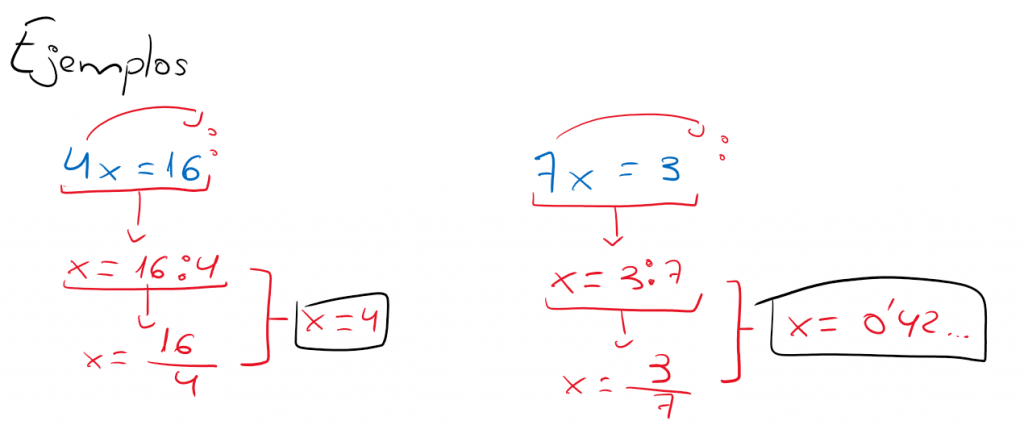
RESOLUCIÓN DE LA ECUACIÓN x:a=b
Para resolver la ecuación x:a=b, multiplicamos la a (para anularla) por a ambos miembros (para mantener la igualdad).
Regla:
Lo que está dividiendo a un miembro (a todo él), pasa multiplicando al otro (esta es la regla que cumple lo leído justo arriba pero de una forma más práctica, por tanto el resultado es el mismo).
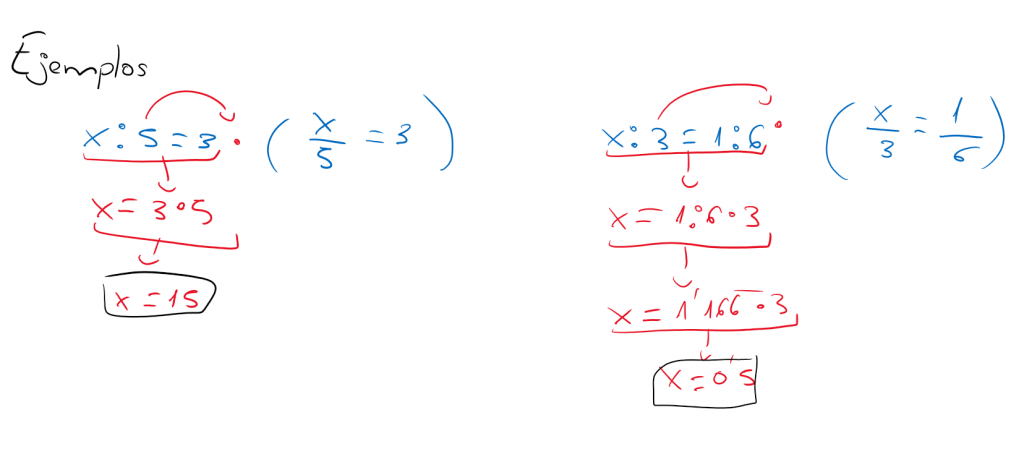
Teoría del tema
Ejercicios resumen
Aquí verás más ejercicios resueltos sobre todo el tema de álgebra tratado en esta entrada: