Blog

REPASO MATEMÁTICAS: números enteros, racionales, irracionales y operaciones.

La información de esta entrada ha sido extraída de los siguientes archivos:

PowerPoint – Presentación de FRACCIONES Y DECIMALESDescarga

JamBoard – Presentación en la pizarra de FRACCIONES Y DECIMALES: https://jamboard.google.com/d/1YZAojiDasOfsbFiFyrJWfJZbFEb_vc0jR-oykXhp-Rg/edit?usp=sharing

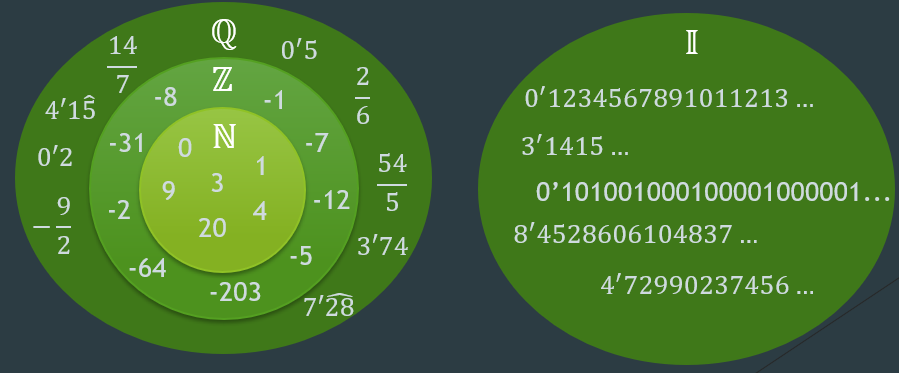
1. TIPOS DE NÚMEROS

  • El conjunto de los números naturales (N): números positivos –> 0, 1, 2, 3, 4, 5, 6…
  • El conjunto de los números enteros (Z): números positivos y negativos –> …-3, -2, -1, 0, 1, 2, 3…
  • El conjunto de los números racionales (Q): números que se pueden expresar en forma de fracción: -1, 0, 1/3, 0’5…
  • El conjunto de los números irracionales (I): números que no se pueden expresar en forma de fracción: 0’123413…
RESUMEN/ESQUEMA

2. REPASO DE LOS Nº ENTEROS

Los números enteros representan los números positivos, negativos y el 0.
Fue necesaria la creación del conjunto de los números enteros cuando los trabajadores del campo que hacían cuentas necesitaron ir más allá de los números naturales, creando así los negativos.

-OPERACIONES CON Nº ENTEROS

SUMAS Y RESTAS:
Para realizar sumas y restas con números enteros, debemos obedecer las siguientes normas: signos iguales se suma y se deja el signo; signos distintos se resta y se deja el signo del mayor: -5+4= -1

PRODUCTOS Y COCIENTES:
Para realizar multiplicaciones y divisiones con números enteros, debemos obedecer las siguientes normas: se opera lo indicado (multiplicación/división) y signos iguales resultado en positivo; signos distintos resultado en negativo: -3·7= -21

OPERACIONES COMBINADAS
Si aparecen las operaciones combinadas, debemos seguir un orden de derecha a izquierda priorizando los corchetes y paréntesis, después potencias y raíces, ahora productos y cocientes y por último sumas y restas: 7+2·2= 7+4= 11

3. NÚMEROS RACIONALES

Los números racionales representan los números que se pueden expresar en forma de fracción, que incluye 0, positivos, negativos, fracciones y algunos decimales.
Este conjunto se creó por la necesidad de representar partes que no alcanzaran la unidad completa.

-LAS FRACCIONES

Una fracción es una división / partes de una unidad.

PARTES DE UNA FRACCIÓN: la parte de arriba forman el numerador; y la inferior, el denominador

-TIPOS DE FRACCIONES

  • PROPIAS: numerador < denominador (representan menos que la unidad): -3/4, 2/7, 5/17…
  • IMPROPIAS: numerador > denominador (representan más que la unidad): -4/3, 7/2, 17/5…
  • ENTERAS: numerador = denominador (representan la unidad, por lo que se consideran un número entero): 7/7, -3/3

SEPARAR FRACCIONES IMPROPIAS EN PARTE ENTERA Y FRACCIÓN
Para separar las fracciones impropias en la parte entera y la que no llega, en fracción, necesitamos realizar una división. El cociente de esta será la parte entera, mientras que el resto será el numerador de la fracción restante (con el mismo denominador que el principio): 7/5= 7:5 –> 1 = 2 + 1/5 = 2 + 1/5.

-FRACCIONES EQUIVALENTES

Las fracciones son equivalentes cuando representan la misma cantidad.
1/2 = 2/4 = 0’5

¿CÓMO SE SABE SI DOS FRACCIONES SON EQUIVALENTES?
Para saber si dos fracciones son equivalentes, conocemos distintos métodos:

  • MULTIPLICANDO EN CRUZ Y OBTENIENTO MISMO RESULTADO: 1/2 = 2/4 (1·4, 2·2 = 4).
  • HACIENDO LAS DIVISIONES (numerador:denominador)Y COMPARARLO: 1/2 –> 1:2 = 0,5 // 2/4 –> 2:4 = 0,5
  • SIMPLIFICARLAS AL MÁXIMO (obtener la irreducible) PARA COMPARARLAS: 1/2 y 2/4 –> 1/2 y 1/2 (:2) =0′,5

¿CÓMO OBTENER DOS FRACCIONES EQUIVALENTES?
Para obtener dos fracciones equivalentes, debemos de operar por el mismo número numerador y denominador.
2/5 –> (2·7)/(5·7) = 14/35

-ORDEN DE FRACCIONES

Según sus numeradores y denominadores, las fracciones se ordenan:

  • MISMO DENOMINADOR: comparar numeradores (– < 0 < +).
  • MISMO NUMERADOR: compara denominadores (mayor denominador < menor denominador).
  • NADA EN COMÚN: reducir a común denominador para comparar numeradores:
    • m.c.m
      • descomposición en factores primos
      • comunes y no comunes al mayor exponente
    • buscar la equivalencia (multiplicar numerador y denominador por el mismo conveniente).

4. OPERACIONES CON FRACCIONES

-SUMAS Y RESTAS

  • Se necesita el común denominador.
  • Operar con los numeradores.

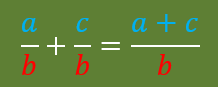
-PRODUCTOS Y COCIENTES

PRODUCTO: multiplicación recta

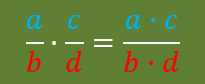
COCIENTE: multiplicación en cruz

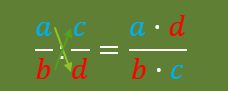
(FRACCIÓN DE OTRA FRACCIÓN)

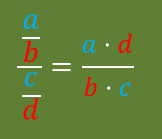
-OPERACIONES COMBINADAS

  • Las fracciones son divisiones.
La imagen tiene un atributo ALT vacío; su nombre de archivo es image-17.png

-PROBLEMAS CON FRACCIONES

FRACCIÓN DE UNA CANTIDAD: a/b de c = c:b·a

REPRESENTAR UNA PARTE CON UNA FRACCIÓN: parte/total –> (simplificar)

AVERIGUAR TOTAL CONOCIENDO LA PARTE: a/b de ? = c –> c·b/a

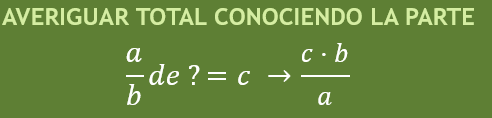
5. NÚMEROS DECIMALES

Los números decimales son partes de la unidad.
*Saber la descomposición de cada decimal permitirá reconocer si una fracción pertenece a un decimal exacto o periódico puro o mixto sin necesidad de realizar la división.

-TIPOS DE DECIMALES

  • DECIMALES EXACTOS: nº de cifras de decimales finita (limitada) –> 0’1, 4’9, 3’5 […]
    • Su descomposición será exclusivamente de 2 y/o 5.
  • DECIMALES PERIÓDICOS: nº de cifras de decimales infinita con período (repetición).
    • DECIMALES PERIÓDICOS PUROS: período justo después de la coma –> 1′(6), 1′(325), 1′(1) […]
      • Su descomposición será de cualquier número menos 2 y 5.
    • DECIMALES PERIÓDICOS MIXTOS: espacio entre la coma y período –> 0’8(3), 7’246(8) […]
      • Su descomposición será una mezcla de cualquier número y 2 o 5.
  • Nº IRRACIONALES: nº no periódicos con infinitos decimales –> 1’123456165432,164…, 0’10100100100001…, 3’1415… […]

-ORDENAR DECIMALES

  • Desarrollar los números.
  • Comprar cada cifra.

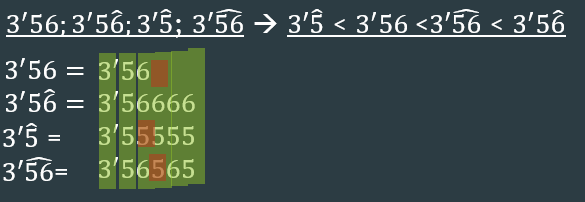
-PASAR DE FRACCIÓN A DECIMAL

Numerador:denominador

-PASAR DE DECIMAL A FRACCIÓN

  • DECIMALES EXACTOS:
    • NUMERADOR: nº entero (sin período) y quitar coma.
    • DENOMINADOR: un 1 seguido de tantos 0 como cifras haya detrás de la coma.
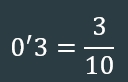
  • DECIMALES PERIÓDICOS PUROS:
    • NUMERADOR: nº entero – nº antes del período y quitar coma.
    • DENOMINADOR: tantos 9 como cifras tenga el período.
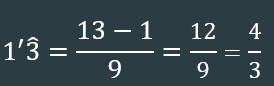
  • DECIMALES PERIÓDICOS MIXTOS:
    • NUMERADOR: nº entero – nºantes del período y quitar coma.
    • DENOMINADOR: tantos 9 como cifras tenga el período seguido de tantos 0 como cifras entre coma y período haya.

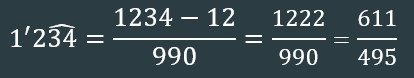
– RECUERDA –

VALOR ABSOLUTO: número resultado sin signo
|-8| = 8 (+8)
|+5| = 5 (+5)

SIMPLIFICACIÓN DE FRACCIONES – REDUCIRLAS: dividir entre el mismo número numerador y denominador.
FRACCIÓN IRREDUCIBLE: no se puede reducir más
5/10 = 1/2

RESULTADOS EN FRACCIÓN: cualquier resultado en forma de fracción debe ser irreducible.

FRACCIÓN DE UNA FRACCIÓN: el «=» marca la separación entre numerador y denominador.

USO DE EXPRESIONES CORRECTAS en los problemas:
28:7 = 4·4 = 16
28:7 ·4 = 4·4 = 16

REDONDEO CALCULADORA: si en la calculadora se repite un número y el último es distinto, se ha redondeado por lo que es infinito.

PASAR DE NÚMERO ENTERO A FRACCIÓN CON COMÚN DENOMINADOR: dejar común denominador y multiplicar el entero por el denominador:
2 + 5/10 = 2/1 + 5/10 = [10·2=20] 20/10 + 5/10 = 25/10 = [simplificar] 5/2

¡Espero que te haya gustado! Más entradas como esta en eva-arnau.es ;).

Deja una respuesta