El significado de las fracciones
Una fracción representa una parte del total. Aquí tienes un ejemplo:
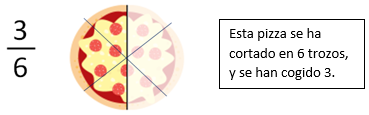
Relación entre fracciones y decimales
Las fracciones son divisiones. Tres sextos (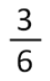
) es lo mismo que decir tres entre seis (3:6).
PASO DE FRACCIÓN DECIMAL:
Para pasar una fracción a decimal, solo hay que hacer la operación que esta indica (dividir):
PASO DE DECIMAL A FRACCIÓN:
La forma de pasar de decimal a fracción es poniendo una barra y un 1 debajo porque los números en sí son fracciones, pero no se indican como tal. 2’31/1 es una fracción con decimales, para quitarlos multiplicamos por tantos ceros como decimales hay: 2’31×100 = 231. Para que sea una fracción equivalente también hay que multiplicar el denominador por el mismo número: 1×100 = 100. Esta es la forma de entenderlo, pero la «fórmula» o forma de hacerlo sin explicación es: poner como numerador (arriba) el número sin coma y de denominador (debajo) un 1 con tantos ceros como cantidad de decimales tenga el numerador, en este caso 2. Por tanto arriba ponemos 231 y abajo 100 (231/100).
¿Cómo calculamos un término desconocido en la igualdad de dos fracciones equivalentes?
Para calcular un término desconocido en la igualdad de dos fracciones equivalentes, conozco dos métodos:
MÉTODO 1: DESPEJAR LA X
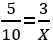
1º: Multiplicamos en cruz (esta es la forma normal de comprobar si dos fracciones son equivalentes, pero con los siguientes pasos también sirve para comprobar si dos fracciones son equivalentes con una X):
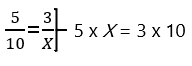
2º: Pasamos la X a la izquierda, haciendo que todas las operaciones estén a la inversa (dividir -> multiplicar / multiplicar -> dividir // sumar -> restar / restar -> sumar). Dicho de otra forma, la X la dejamos sola, para ello tenemos que apartarla del resto de números al lado contrario (la derecha en este caso) y entonces operar a la inversa de lo que sería:
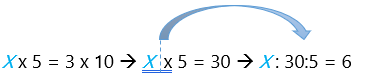
Parece complicado pero es más que nada práctica, para dejar la X sola en este caso apartamos el x5 al otro lado del igual, de tal forma que se convierte en un :5. Siempre que se pasa al otro lado del igual ha de ser al final, es decir, si x5 lo pasamos al otro lado del igual habiendo un 30, será X = 30:5, porque el :5 irá detrás.
MÉTODO 2: USAR LA «LÓGICA»
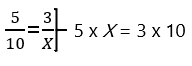
1º: Primero hacemos el lado del igual que podemos (el que no tiene X) para ver qué número debe dar el otro lado del igual, es decir: X x 5 = 3 x 10, por tanto X x 5 = 30.
2º: Para saber cuál es la X, debe dividirse el resultado del otro lado del igual entre el número por el que se multiplica la X, en este caso 30:5 = X, porque al dividir 30:5 el resultado es el número multiplicado por 5 es igual a 30, básicamente X.
Fracciones equivalentes
Las fracciones equivalentes son aquellas que expresan la misma cantidad siendo distintos números. Aquí tienes una representación gráfica:
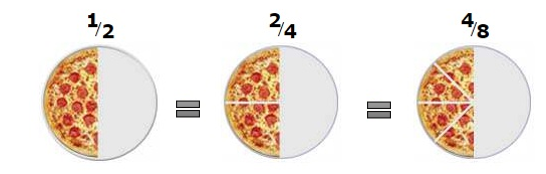
¿Cómo obtenemos fracciones equivalentes?
Para que dos fracciones sean equivalentes, hay que multiplicar o dividir el numerador y el denominador por el mismo número. Cuando se divide numerador y denominador por el mismo número, se está simplificando.
¿Cómo averiguamos si dos fracciones son equivalentes?
Para saber si dos fracciones son equivalentes, podemos expresarlas gráficamente (dibujarlas si no son demasiado altas) o si al multiplicar en cruz el numerador y denominador de la nueva fracción es el mismo, es decir una unidad (porque se cogen todas las partes de todas las partes que hay):
Reducción a común denominador
Sabemos operar con fracciones de mismo denominador (número inferior a la línea), pero, si tienen distinto denominador, ¿cómo operamos con ellas? Para operar con fracciones de distinto denominador hay que conseguir que ambas tengan el mismo, respetando la equivalencia de cada una de las fracciones. Para que sea el mismo resultado, debemos conseguir que tengan mismo denominador haciendo uso de fracciones equivalentes, pues ocupan el mismo espacio como ya hemos visto anteriormente.
1º: Hacemos el mínimo común múltiplo (si no sabes cómo se hace, tengo una página donde lo explico: https://eva-arnau.es/2020/06/21/la-divisibilidad-numeros-primos-y-compuestos-descomposicion-en-factores-primos/) de los denominadores:
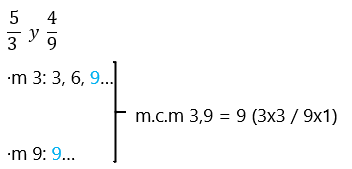
2º: Ponemos como denominador de las fracciones el mínimo común múltiplo de ambos números, y para que la fracción continúe siendo equivalente, multiplicamos el numerador por el mismo que multiplicamos el denominador de cada fracción (como ya hemos visto, al multiplicar o dividir numerador y denominador de una fracción por el mismo número, creamos una fracción equivalente, es decir que representa el mismo espacio siendo distinta) (5/3 hemos multiplicado 3×3 para que de 9 que es el denominador común de las dos fracciones, por tanto hemos de hacer 5×3. De igual forma, en la otra fracción hicimos 9×1 para poner de denominador el común de las dos fracciones, por tanto el numerador (4) debe multiplicarse por el mismo número (1).
Operaciones combinadas
Para hacer operaciones combinadas con fracciones, obedecemos el orden mismo cuadro que se utiliza para realizarlas sin fracciones:
1º: Paréntesis y corchetes.
2º: Potencias y raíces.
3º: Multiplicaciones y divisiones.
4º: Sumas y restas.
Ese orden es el que se debe seguir para hacer operaciones combinadas:
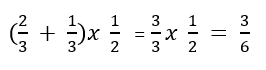
Primero realizamos paréntesis (no hay corchetes), 2/3+1/3, el resultado lo multiplicamos por 1/2 (porque no hay división ni potencia o raíz que se hacen antes). Al tener distinto denominador hay que hacer la reducción a común denominador que leíste anteriormente. Como no hay más operaciones (después de esto se harían sumas o restas, pero no hay).