¡Bienvenido a una nueva entrada! Aquí encontrarás la teoría sobre las ecuaciones de primer grado.
Antes de empezar, puedes descargar estos archivos con todo lo que hay en la entrada para repasar offline:
1. Significado y utilidad
- Ecuación: expresa con una igualdad algebraica una relación entre cantidades que de momento desconocemos (incógnitas).
2. Elementos y nomenclatura
- Miembros: igualdades que hay a cada lado del igual:
- 1º miembro: lo que hay a la izquierda del igual.
- 2º miembro: lo que hay a la derecha del igual.
- Términos: cada elemento que suma o resta que forman los miembros.
- Incógnitas: letras que aparecen en la ecuación que representan un valor que desconocemos.
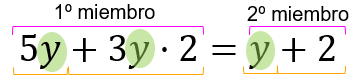
- Soluciones: valor que tiene la incógnita para que la igualdad sea cierta.
- Grado: el mayor de los exponentes a los que está elevado la parte literal.
- Ecuaciones equivalentes: tienen mismas incógnitas y mismas soluciones.
- Comprobación: sustituir la incógnita por la solución y comparar los resultados (ambos miembros deben dar lo mismo)
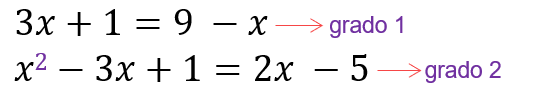
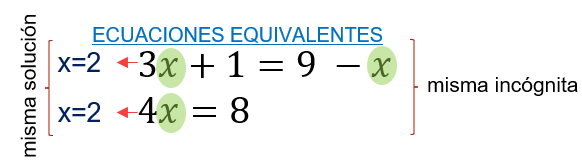

3. Transposición de términos
- Transposición de términos: nos permite convertir las ecuaciones en otras más sencillas.
- Cuando sumamos/restamos/dividimos/multiplicamos el mismo número en cada miembro de la ecuación, obtenemos una ecuación equivalente.
- Para transponer términos de un miembro a otro hay que tener en cuenta:
- SUMANDO = RESTANDO
- RESTANDO = SUMANDO
- MULTIPLICANDO = DIVIDIENDO
- DIVIDIENDO = MULTIPLICANDO
4. Resolución de ecuaciones
- (Si hay paréntesis):
- quitarlos
- (Si hay fracciones):
- obtener mismo denominador en todos los términos (m.c.m)
- tachar todos los denominadores una vez sean iguales
- Transponer:
- términos con x –> 1º miembro
- términos sin x –> 2º miembro
- Reducir
- Despejar
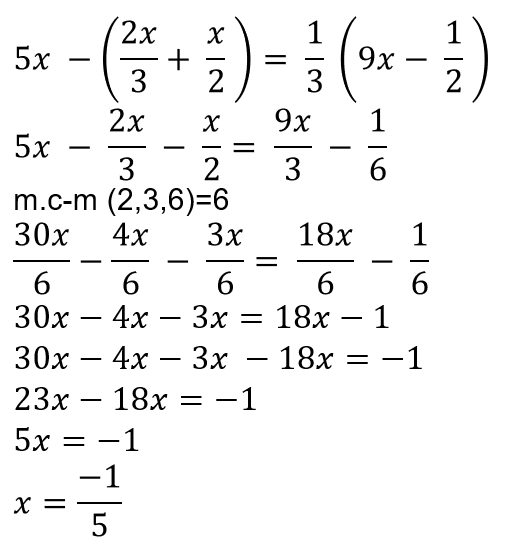
¡Espero que te haya gustado! Más entradas como esta en eva-arnau.es ;).
