Números divisibles por otros
Un número es divisible por otro si al dividirlos el resultado es exacto.
–Ejemplo: 20:2 = 10 (sin resto) -> 20 es divisible entre 2.
Múltiplos
Los múltiplos de un número son los resultados de este multiplicado por otros:
–Ejemplo: múltiplos de 20 -> 20 (20×1), 40 (20×2), 60 (20×3), 80 (20×4), 100 (20×5)… *Son infinitos.
Criterios de divisibilidad
Para saber cuáles son o no múltiplo de un número, no es necesario ir probando todos. Aquí hay algunos que se pueden conseguir saber sin tener que hacer la división.
- Divisibilidad por 2:
- Un número es múltiplo de 2 si termina en cifra par: 0-2-4-6-8
- Divisibilidad por 3 y 9:
- Un número es múltiplo de 3 si la suma de sus cifras es múltiplo de 3:
- 39: es múltiplo de 3 porque 9+3 = 12, y 3·4 = 12.
- Un número es múltiplo de 9 si la suma de sus cifras es múltiplo de 9:
- 612: es múltiplo de 9 porque 6+1+2 = 9, y 9·1=9.
- Un número es múltiplo de 3 si la suma de sus cifras es múltiplo de 3:
- Divisibilidad por 5 y 10:
- Un número es múltiplo de 5 si termina en 0 o 5.
- Un número es múltiplo de 10 si termina en 0.
- Divisibilidad por 11:
- Un número es múltiplo de 11 si la suma de sus cifras de lugar par menos la suma de sus cifras de lugar impar es igual a 0 o múltiplo de 11:

Números primos y compuestos
Un número es primo cuando de divisores sólo se tiene a sí mismo y a la unidad: 7 es un número primo porque sus únicos divisores son el 1 y el 7.
Un número es compuesto cuando tiene más de dos divisores: 6 es un número compuestos porque sus divisores son 1, 2, 3 y 6.
Descomposición de un número en sus factores primos
Para descomponer un número en sus factores primos (descomposición factorial o factorizar), hay que seguir unos pasos:
- –Colocar el número junto a una línea vertical al lado:
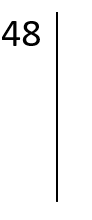
- –Poner el menos número primo por el que se pueda dividir y el resultado en la parte de la izquierda, así hasta que no se pueda dividir por el mismo número, que se cambiaría por el siguiente que se pueda hasta llegar al 1, que se dejaría sin número a la derecha:

- –Convertir los resultados (números de la derecha) en potencias, y eso será lo mismo que el número principal:
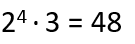
Mínimo común múltiplo de dos números
El mínimo común múltiplo de dos números es el múltiplo más pequeño común entre los números que comparemos, y se puede hacer de dos formas:
- MÉTODO 1 (para números dentro de las tablas conocidas):
- Poner múltiplos de cada número (x·1, x·2, x·3…).
- MÉTODO 2 (para números «grandes»):
- Hacer la descomposición en factores primos de los números, coger los números (bases) de las potencias (sin repetirlos, solo una vez cada uno), y ponerle de exponente a cada uno el mayor exponente aparecido en cada potencia.

- Hacer la descomposición en factores primos de los números, coger los números (bases) de las potencias (sin repetirlos, solo una vez cada uno), y ponerle de exponente a cada uno el mayor exponente aparecido en cada potencia.
Máximo común divisor de dos números
El mínimo común múltiplo de dos números es el divisor común mayor entre los números que comparemos, y se puede hacer de dos formas:
- MÉTODO 1 (para números dentro de las tablas conocidas):
- Poner divisores de ambos números (x:a, x:b, x:c…)

- Poner divisores de ambos números (x:a, x:b, x:c…)
- MÉTODO 2 (para números «grandes»):
- Hacer la descomposición factorial de los números, coger los resultados en común con el menor exponente y operar:
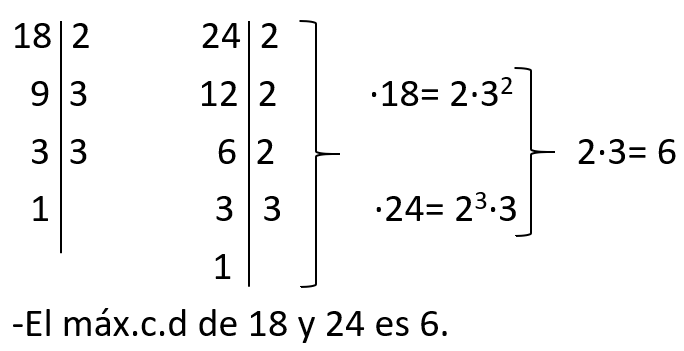
- Hacer la descomposición factorial de los números, coger los resultados en común con el menor exponente y operar:

Pingback: itemprop="name">Matemáticas: fracciones y operaciones combinadas – Web de Eva Arnau
Pingback: itemprop="name">Álgebra: teoría y ejercicios resueltos. – Web de Eva Arnau
Pingback: itemprop="name">Matemáticas: los números naturales – Web de Eva Arnau